
4.1.1 Le traitement spectral des champs horizontaux
Les équations primitives données précédemment n'admettent pas de solution analytique. La méthode spectrale consiste à représenter un champ sous la forme d'un développement en séries de fonctions connues et judicieusement choisies. Ainsi pour un champ X, on écrira :

Remarque : En théorie la somme est infinie mais dans la pratique on tronque le développement ( limitation du calculateur ).
La connaissance de X en tous points de l'espace est remplacée par la connaissance des coefficients Xk.
La résolution du système d'équations primitives revient à déterminer les équations d'évolution pour chacun des Xk. La géométrie sphérique de la terre et de la pellicule atmosphérique conduit à utiliser des fonctions définies sur la sphère.
4.1.1.1 Les harmoniques sphériques de surface
On utilise comme fk, les fonctions propres de l'opérateur Laplacien sur la sphère. Ces fonctions forment une base orthogonale pour l'ensemble des fonctions continument différentiables sur la sphère et possèdent des propriétés qui simplifient les calculs.
Chaque champ peut s'écrire au point de coordonnées ( lambda,µ = sin théta )

Les Ynm sont les fonctions de Laplace ou harmoniques sphériques de surface ( fonctions complexes ).
La recherche des fonctions propres de l'opérateur Laplacien sur la sphère conduit, en séparant les variables à écrire les fonctions Ynm sous la forme :

Les Pnm définis sur [-1; 1] sont les polynômes de Legendre ( réels ). Les fonctions complexes Ynm bien connues, sont choisies de façon à être orthonormées c'est-à-dire :

La discrétisation du problème conduit à définir
une troncature c'est-à-dire à choisir un couple
( M, N ) auquel sera restreinte la définition
des variables.
Dans ARPEGE on utilise une troncature triangulaire
( soit M = N ) de 119 depuis décembre 1993, ce qui signifie :

L'intérêt de la troncature triangulaire est son isotropie : la valeur d'une fonction tronquée triangulairement à l'ordre M garde cette propriété dans tout changement de repère de coordonnées sphériques, bien que l'expression des coefficients spectraux soit modifiée. Cette propriété est importante pour le modèle opérationnel ARPEGE.
4.1.1.2 Les transformations spectrales
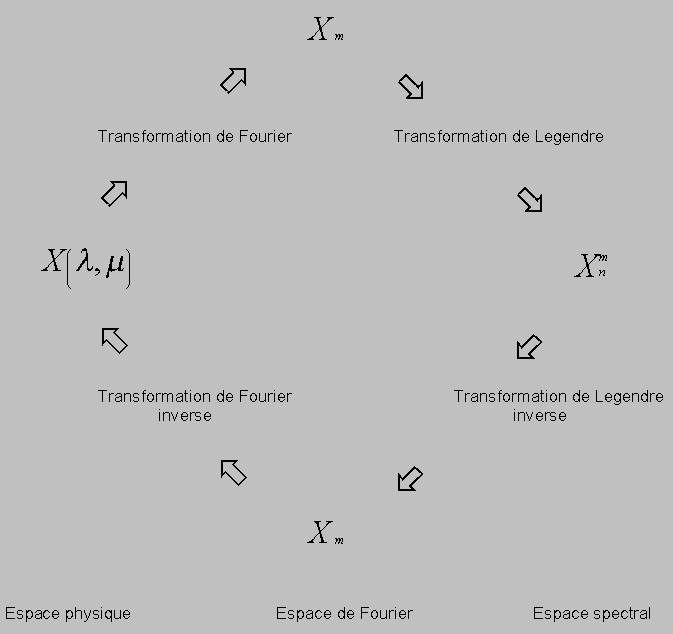

A partir du champ en points de grille, les coefficients de Fourier sont déterminés par

et les coefficients spectraux par

on a alors :

Pour calculer ces coefficients spectraux Xnm, on utilise la transformation de Fourier et la quadrature de Gauss. La quadrature de Gauss est le remplacement d'une intégrale par une somme finie, elle introduit les poids et les latitudes de Gauss définis par :

Toutes ces transformations ( Fourier, Fourier inverse, Legendre, Legendre inverse ) sont bien connues du Cray et donc effectuées très rapidement à la précision de l'ordinateur.
4.1.1.3 La grille de Gauss associée
Pour une troncature donnée, il existe une grille optimale de points ( en latitude et longitude ) sur la sphère qui permet de calculer la valeur exacte des coefficients spectraux et des termes quadratiques à la précision de l'ordinateur ( utilisation des transformations de Fourier et de la formule de la quadrature de Gauss ).La grille réduite de Gauss associée au modèle ARPEGE actuel ( T119 ) possède :
- 180 cercles de latitude ; 180 et non 179 car ce nombre doit être pair sous peine d'avoir un cercle de latitude à l'équateur et de ne pouvoir y définir 1/f.Remarques :
- L'intérêt de la méthode spectrale est qu'elle permet d'évaluer exactement ( à la précision de l'ordinateur près ) les dérivées spatiales et de calculer ainsi le déplacement de ces ondes sans erreur de phase contrairement à ce qui pouvait être obtenu avec le calcul en différences finies. Cette méthode permet de supprimer le ralentissement systématique de la vitesse de propagation des dépressions ( dans le cas du calcul en différences finies ). En revanche, l'erreur sur cette prévision est devenue plus aléatoire, la vitesse de propagation peut être parfois nettement surestimée.
- La représentation spectrale des champs horizontaux fait apparaître une superposition d'ondes que les études de la circulation générale de l'atmosphère ont rendu familières : La dépendance en lambda ( µ fixé ) montre que m peut être interprété comme un nombre d'onde zonal ( nombre de 0 de la fonction Pnm sur un cercle de latitude ). D'après les propriétés des polynômes de Legendre, on montre que n-|m| peut être interprété comme un nombre d'onde méridien, on peut donc assimiler n à un nombre d'onde global.
- La méthode spectrale utilise pour le calcul des termes non linéaires des équations, la grille de Gauss réduite, cette dernière sert ensuite aux calculs ponctuels, nécessaires à la prise en compte des effets des paramétrisations physiques.

| 
|
|---|